یادآوری مفهوم تابع
تابع یک رابطهٔ خاص بین دو مجموعه است که هر عنصر از مجموعهٔ اول (دامنه) را به یک و تنها یک عنصر از مجموعهٔ دوم (برد) نسبت میدهد.
🔹 ۱. تعریف تابع
مثال: فرض کنید مجموعه A = {۱, ۲, ۳} و B = {۴, ۵, ۶}.
رابطه f = {(۱, ۴), (۲, ۵), (۳, ۶)} یک تابع است، چون هر عنصر A دقیقاً به یک عنصر B نسبت داده شده است.
رابطه f = {(۱, ۴), (۲, ۵), (۳, ۶)} یک تابع است، چون هر عنصر A دقیقاً به یک عنصر B نسبت داده شده است.
⚠️ اگر یک عنصر از دامنه به دو عنصر از برد نسبت داده شود، دیگر تابع نیست!
🔹 ۲. نمایش پیکانی
در این نمایش، عناصر دامنه و برد را در دو ستون قرار میدهیم و با پیکانها به هم وصل میکنیم.
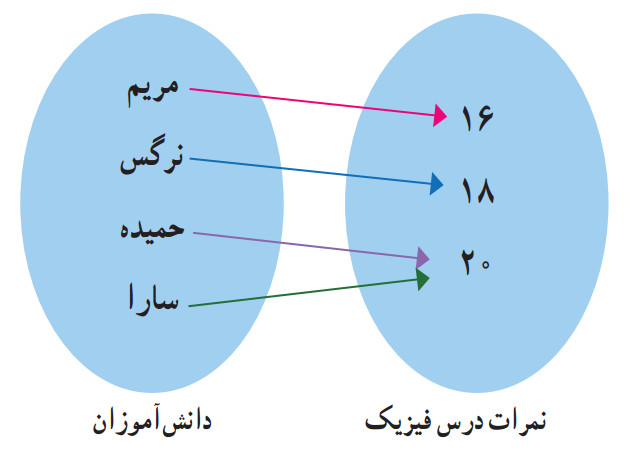
✅ نکته: هر عنصر دامنه باید دقیقاً یک پیکان داشته باشد.
🔹 ۳. نمایش جدولی (x سمت چپ)
در این نمایش، مقادیر x را در ستون سمت چپ و مقادیر y را در ستون سمت راست مینویسیم.
| x | y = f(x) |
|---|---|
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
✅ نکته: هیچ x دوباره تکرار نشده است — یعنی هر x یک y دارد.
🔹 ۴. نمایش زوج مرتبی
تابع را میتوان بهصورت مجموعهای از زوجهای مرتب نوشت:
f = {(1, 4), (2, 5), (3, 6)}
✅ نکته: هیچ دو زوج مرتبی نباید دارای عضو اول (x) یکسان باشند.
🔹 ۵. نمایش نموداری
در این نمایش، نقاط (x, y) را در صفحهٔ مختصات رسم میکنیم.
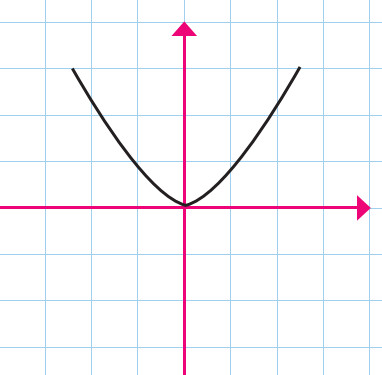
✅ نکته: اگر خط عمودی از هر نقطه x بزنیم، فقط یک نقطه از نمودار را قطع کند — آنگاه تابع است (آزمون خط عمودی).
🔹 ۶. نمایش ضابطهای
تابع را با یک فرمول ریاضی بیان میکنیم:
f(x) = x + 3
یعنی برای هر x، y برابر با x + 3 است.
f(1) = 1 + 3 = 4
f(2) = 2 + 3 = 5
f(3) = 3 + 3 = 6
f(2) = 2 + 3 = 5
f(3) = 3 + 3 = 6
✅ نکته: ضابطه میتواند ساده (مثل x+3) یا پیچیده (مثل √x یا sin(x)) باشد.
🎯 خلاصه
• تابع: هر عنصر دامنه به یک و تنها یک عنصر برد نسبت داده میشود.
• نمایشهای مختلف: پیکانی، جدولی، زوج مرتبی، نموداری، ضابطهای.
• برای تشخیص تابع در نمودار، از آزمون خط عمودی استفاده کنید.
• نمایشهای مختلف: پیکانی، جدولی، زوج مرتبی، نموداری، ضابطهای.
• برای تشخیص تابع در نمودار، از آزمون خط عمودی استفاده کنید.
تمرین تشخیص تابع با تصاویر نمودارهای پیکانی
در این تمرین، باید تشخیص دهید که آیا رابطهی ارائه شده در هر نمایش، تابع است یا خیر.
در سوالات نمودار پیکانی، از تصاویر واقعی استفاده شده است.
تعریف تابع: رابطهای از مجموعه A به مجموعه B را تابع مینامیم هرگاه هر عضو از مجموعه A به یک عضو منحصربهفرد از مجموعه B مربوط شود.
نتیجه تمرین
0/0
لطفاً پاسخ تمام سوالات را وارد کنید.